更新日志
[2021年7月9日] 开始更新训练二题解,今天先上难度1的题,正好题目简单,可以让大家领会一下Python的优雅。之后的题目也都会有Python版本(因为太好用了,毕竟是小训练问题不大),同时考虑到兼顾的问题,也会向朋友们征集C++版本的代码进行发布。如果想要某题的C++代码也可以在下方评论区留言,我有时间就手敲。
[2021年7月11日] 更新了难度2的题目,之后参考代码都是Python的,无论有无基础,认真看都是能看懂的。
[2021年7月14日] 已更新所有题目的题解。
[2021年9月5日] 训练三题解已更新,点此<传送门>进入。
本文只有第7、12、21题使用了C++编写,若需其他题目的C++思路,点击这里查看森大的文章。
前言
文章内容为作者个人学习心得,解题思路及参考代码不一定是最优的,如发现有不正确的地方或更优的解法,欢迎批评指正或讨论交流,联系方式可以在页面下方找到。
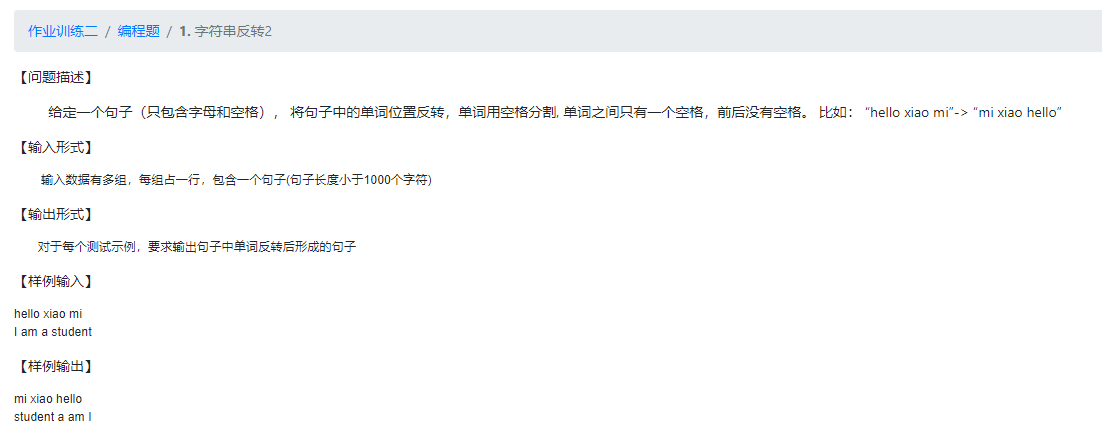
1.字符串反转2
思路: 由于数据的条数不明,故使用while循环。处理方式就是将字符串以空格符进行分割得到由每个单词组成的列表,之后对列表进行逆序操作,最后用空格符将单词连成句子并输出。
try:
while True: # 持续循环
sentence = input()
temp = sentence.split(" ") # 以空格符分割字符串得到单词列表
temp.reverse() # 将单词列表逆序
sentence = " ".join(temp) # 拼接成句子
print(sentence) # 输出逆序后的句子
except EOFError: # 若已经到输入的结尾EOF则退出
pass2.487-3279

思路:删除输入数据中的'-',然后按照映射表对字母进行替换,最后在第三个数字后加上'-',得到正确格式的电话号码。判断列表中是否已存在该电话号码,若已存在则计数加1,若不存在则将电话号码加入列表中,重复上面的操作。最后将出现次数大于1的电话号码按字典序输出即可。
n = int(input())
numbers = [] # 电话号码
count = [] # 电话号码出现的次数
# 映射表
map = {'A': '2', 'B': '2', 'C': '2', 'D': '3', 'E': '3', 'F': '3', 'G': '4', 'H': '4', 'I': '4', 'J': '5', 'K': '5', 'L': '5',
'M': '6', 'N': '6', 'O': '6', 'P': '7', 'R': '7', 'S': '7', 'T': '8', 'U': '8', 'V': '8', 'W': '9', 'X': '9', 'Y': '9'}
for i in range(n):
temp = input().replace("-", "") # 去除输入中的"-"
for j in range(len(temp)): # 按照映射表对字母进行替换
if temp[j] in map:
temp = temp.replace(temp[j], map[temp[j]])
num = "-".join([temp[:3], temp[3:]]) # 在第三个数字后边加上"-"
if num not in numbers: # 判断这个电话号码是否已经存在
numbers.append(num) # 若不存在则加入列表中
count.append(1)
else:
count[numbers.index(num)] += 1 # 否则该电话号码的计数加1
result = [] # 存放待输出的结果
for i in range(len(numbers)):
count[i] = str(count[i]) # 将计数转为字符串类型
if count[i] != '1': # 将出现次数大于1的号码加入待输出列表中
result.append([numbers[i], count[i]])
result.sort(key=lambda x: x[0]) # 按从小到大排序
for i in result:
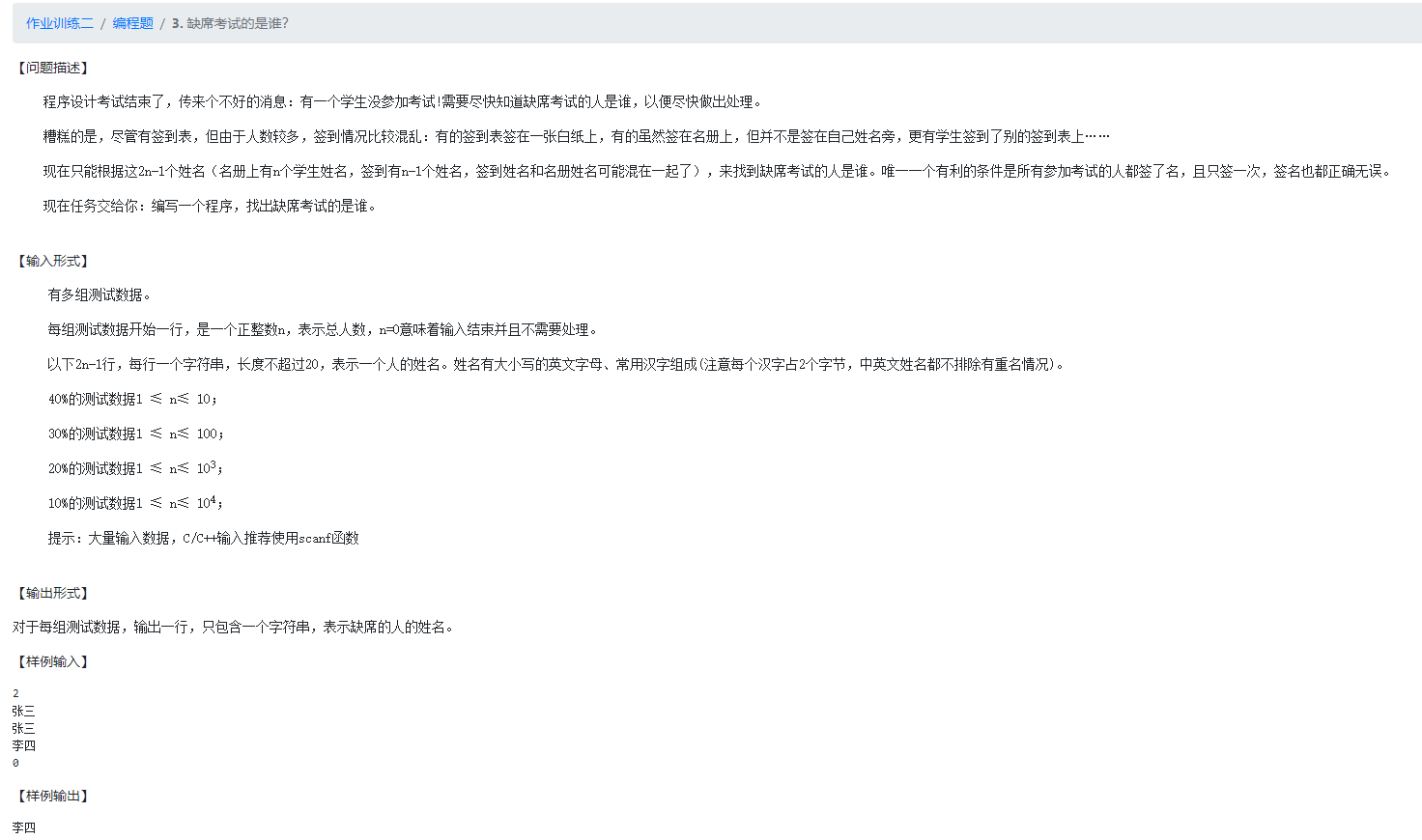
print(" ".join(i))3.缺席考试的是谁?
思路:缺席的人的名字出现的次数必为奇数。
while True: # 读取数量不确定的数据
n = int(input())
if n == 0: # 遇0退出
break
names = {} # 名字字典,{"姓名":出现次数}
for i in range(2*n-1): # 读取接下来的2n-1行
temp = input()
names[temp] = names.get(temp, 0)+1 # 若名字第一次出现则加入字典且赋值为1,若不是则在原有值上加1
for i in names:
if names[i] % 2 != 0: # 由于只有1人缺席,且会出现重名的情况,那么缺席的人的名字出现的次数必为奇数
print(i)
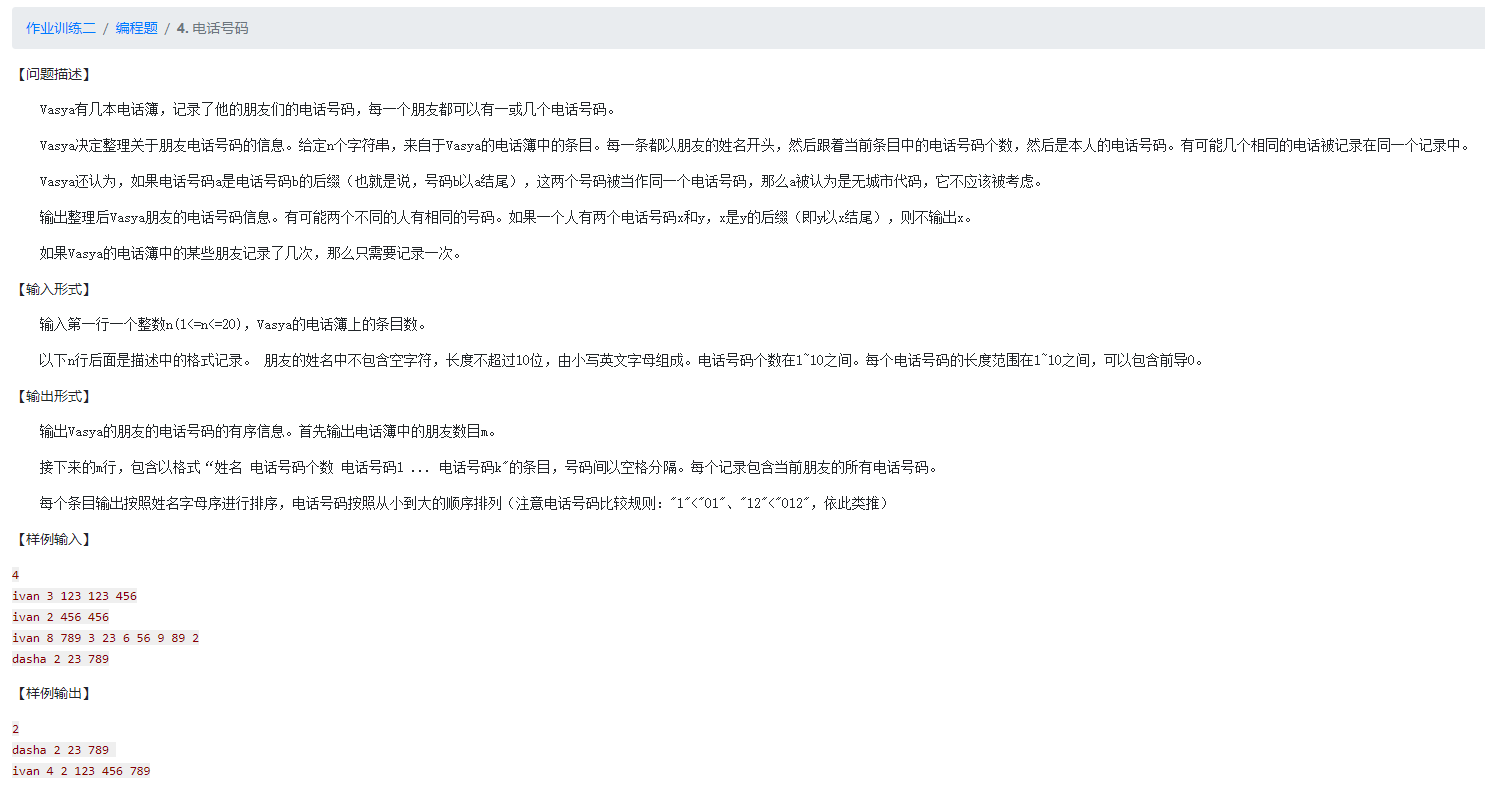
break4.电话号码
思路:这题按照代码注释的方向走方便理解。
n = int(input())
names = [] # 记录联系人姓名
numbers = [] # 记录联系人电话号码
for i in range(n):
temp = input().split(" ") # 以空格符分割输入数据
name = temp[0]
num = temp[2:] # 从[下标]为2到结尾,均为电话号码
if name not in names: # 若名字第一次出现,存储数据
names.append(name)
numbers.append(num)
else: # 否则只将电话号码逐个加入对应位置的列表中
numbers[names.index(name)].extend(num)
for i in range(len(numbers)): # 使用集合的特性对电话号码去重
numbers[i] = list(set(numbers[i]))
for i in range(len(numbers)):
index = []
for j in range(len(numbers[i])):
for k in range(len(numbers[i])):
if j == k:
continue
else:
if numbers[i][j] in numbers[i][k]: # 若某个电话号码包含在另一个电话号码中
# 且是它的后缀
if numbers[i][k][len(numbers[i][k])-len(numbers[i][j]):] == numbers[i][j]:
index.append(j) # 记录j的下标,之后将j位置的电话号码删除,因为它不符合题意
index = list(set(index)) # 去除重复记录的下标
index.sort() # 对下标从小到大排序,方便删除元素
temp = 0 # 由于pop后下标会改变,所以要设置一个偏移量
if(len(index) != 0):
for q in index:
numbers[i].pop(q-temp) # 删除是后缀的电话号码
temp = temp+1
data = []
for i in range(len(numbers)):
numbers[i].sort(key=lambda x: (len(x), x)) # 对电话号码排序,由于'1'在'01'之前,只需先按字符串长度升序排列,再按数字升序排列即可
temp = [names[i]] # 构造列表,结构为[姓名,电话号码个数,电话号码1,电话号码2,...]
temp.append(str(len(numbers[i])))
temp.extend(numbers[i])
data.append(temp) # 加入数据列表中等待输出
data.sort(key=lambda x: x[0]) # 按姓名的字典序排序
print(len(data))
for i in data:
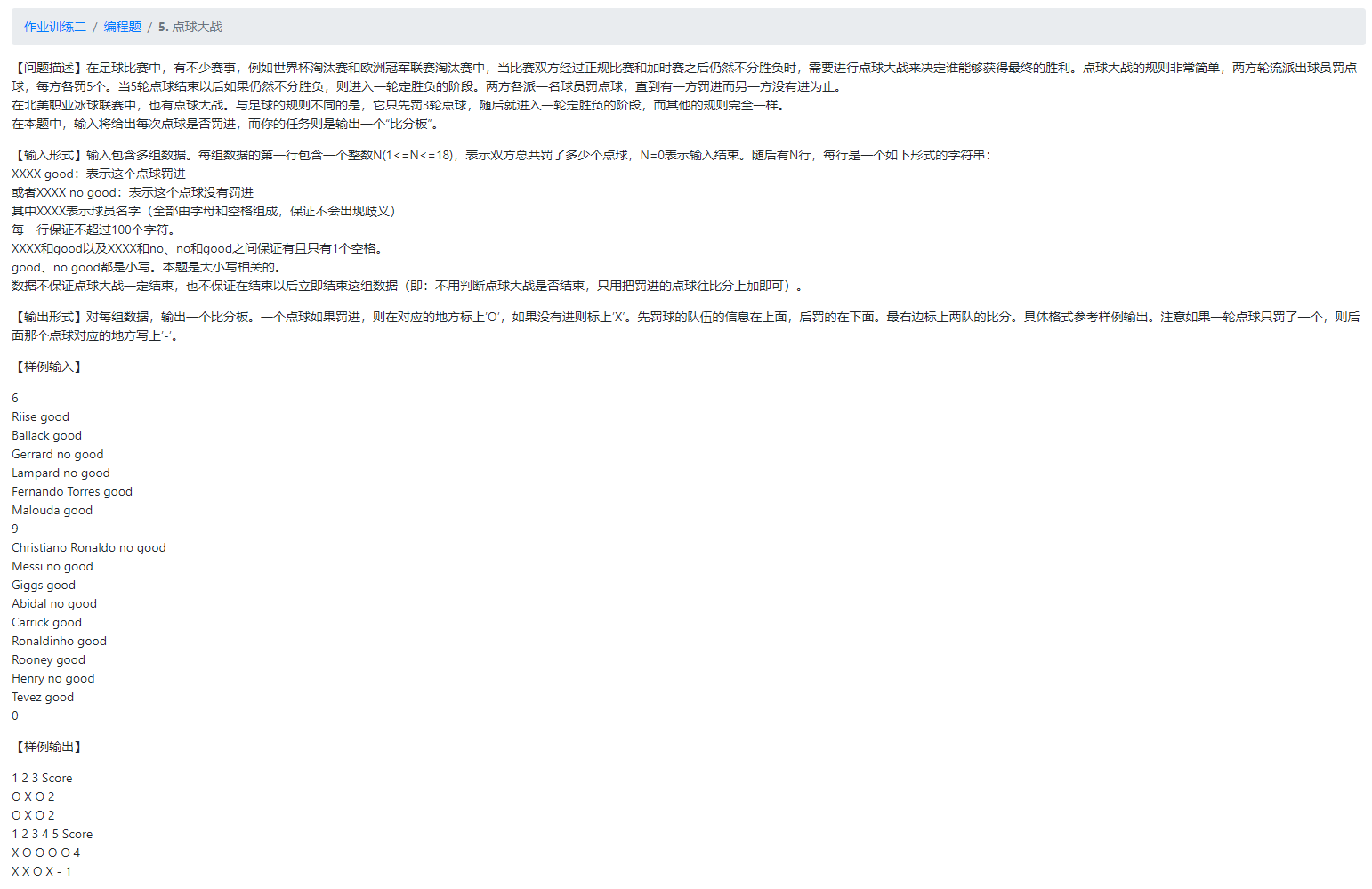
print(" ".join(i))5.点球大战
思路:人名不需要用到,按输入行数判断该队员是甲队还是乙队,通过判断字符串是否含有"no good"来记录点球得失,通过判断双方点球的个数是否相等来看是否要补上"-"。
while True:
n = int(input())
if n == 0: # 遇0退出
break
result = [[], []] # 比赛结果,结构为[[甲队得分情况],[乙队得分情况]]
for i in range(n):
temp = input()
flag = 'O'
if "no good" in temp: # 如果字符串中含有"no good"则代表未进球
flag = 'X'
else:
flag = 'O'
if i % 2 == 0: # 若输入数据的行数为偶数(从0开始),则该数据对应甲,否则对应乙
result[0].append(flag)
else:
result[1].append(flag)
if len(result[0]) < len(result[1]): # 若存在某队少点一个球的情况,则补上"-"
result[0].append('-')
elif len(result[0]) > len(result[1]):
result[1].append('-')
first = [str(x+1) for x in range(len(result[0]))] # 按照点球数量生成表头"1 2 3 ... Score"
first.append("Score")
print(" ".join(first))
score1 = str(result[0].count('O')) # 统计甲点进球的个数
result[0].append(score1)
score2 = str(result[1].count('O')) # 统计乙点进球的个数
result[1].append(score2)
print(" ".join(result[0]))
print(" ".join(result[1]))6.飞行棋
思路:注意骰子点数是对L和Y依次生效的,特殊格子存在连跳的可能,到终点后返回的情况也会碰到特殊格子。(经提醒,还需考虑棋子被吃的情况。)
try:
while True: # 持续循环
A, B, C = input().split(" ")[1:] # 读入A,B,C
A = int(A)
B = int(B)
C = int(C)
board = input().split(" ") # 读入棋盘
winer = "" # 胜利者
flag = 1 # 1则L动,2则Y动
point = C # 递推式变量
indexL = 0 # L的位置
indexY = 0 # Y的位置
while winer == "": # 当未决出胜负时
point = (A*point+B) % 6+1 # 计算骰子点数
if flag == 1: # 如果轮到L动
if indexL+point < len(board)-1: # 移动后未达到终点
indexL += point # 坐标增加
while "G" in board[indexL]: # 判断移动后是否位于特殊格子
indexL = int(board[indexL][1:]) # 取出瞬移到的坐标
flag = 2 # 轮到Y动
elif indexL+point == len(board)-1: # 移动后恰好到达终点
winer = "Lele" # 记录胜利者
else: # 移动后需要从终点返回
indexL = len(board)-1 - \
(point-(len(board)-1-indexL)) # 计算返回后到达的坐标
while "G" in board[indexL]: # 判断移动后是否位于特殊格子
indexL = int(board[indexL][1:])
flag = 2 # 轮到Y动
else: # 如果轮到Y动,原理同上
if indexY+point < len(board)-1:
indexY += point
while "G" in board[indexY]:
indexY = int(board[indexY][1:])
flag = 1
elif indexY+point == len(board)-1:
winer = "Yueyue"
else:
indexY = len(board)-1-(point-(len(board)-1-indexY))
while "G" in board[indexY]:
indexY = int(board[indexY][1:])
flag = 1
print(winer)
except EOFError: # 若已经到输入的结尾EOF则退出
pass7.棋盘
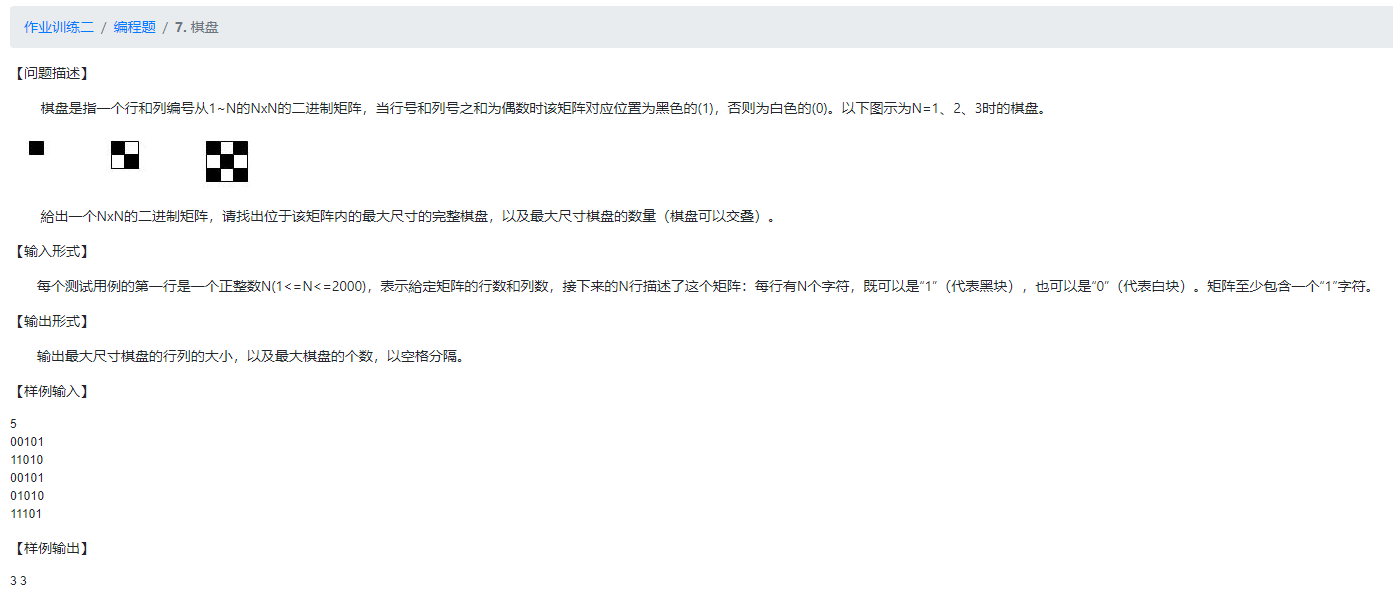
(这一题是我研究得最久的一题,它本身并不难,只是某天突发奇想,想使用非常规的方法来解决,就深入思考了下,之前用的是Python写,一直超时,还为此学了很多优化技巧但依旧救不回,后来用C++,本地跑超大规模秒出,放到CG上就会超时最后一个数据,又去学了C++的优化技巧,也是救不回,所以第一个方法只适合学习新思路用,要AC就得用第二个方法的代码。常见的解法有递归法、暴力搜索法等,递归确实好用但是理解起来有些困难,暴力搜索法比较简单速度也还行,我自己想到的新方法是拟卷积法,这个方法速度比暴力搜索法慢,但是思路很有意思。)


思路:因为原理和卷积不太相同但却相似,所以叫它拟卷积法。对于每个格子,如果1或0出现在了它们的正确位置上,则赋予相应的权值,若位于错误位置上,就减去相应权值的整数倍作为惩罚。这样如果棋盘的某一小部分与该阶数的正确拟卷积核的期望值相等可视为这一部分棋盘是符合预期的,且由于是从大到小对结束遍历,此时找到了一个符合预期的棋盘则是最大尺寸棋盘,统计该尺寸的符合预期的棋盘的数量即为所求。
拟卷积法(会超时一个样例)
#include <iostream>
using namespace std;
int main(){
int n;
cin >> n;
char board[n][n]; //输入的棋盘数据
for (int i = 0; i < n; i++) cin >> board[i];
int maxn = 0, count = 0, flag = 1, startn = 0, startm = 0, d = 0, kernelvalue = 0, tempvalue = 0; //分别是最大棋盘尺寸,最大数量,遍历结束标识,开始的行数,开始的列数,相对于第一行的偏移,拟卷积核期望值,拟卷积核在棋盘上滑动时的实际值
for (int i = n; i > 0; i--){ //要找最大尺寸,所以阶数从n开始到0遍历
startn = 0;startm = 0;d = 0; //每遍历一个阶都要初始化这些变量
if (flag == 0) break; //若标识符为0则表明已经找到最大尺寸且统计完成,可以退出
int white = 0, foot = 0, loop = 1; //拟卷积核的白色格子数,递归等差递推公式的公差,公差增加的周期为2,当loop为2时公差比原先增加2
for (int j = 1; j < i + 1; j++){white += foot;loop++;if (loop == 2){foot += 2;loop = 0;}} //计算当前阶数的拟卷积核的白色格子数
kernelvalue = (i * i - white) * 42 + white; //对于白色格子赋权重为1,黑色格子赋权重为42,计算出拟卷积核的期望值,后续用于对比,若与期望值相等则表明棋盘符合要求
while (1){ //一直查找,直到找到为止
tempvalue = 0;
for (int a = startn; a < startn + i; a++){ //行数遍历
for (int b = startm; b < startm + i; b++){ //列数遍历
//if(tempvalue<0) break; 加上这行就和硬查找算法一样了,为了体现卷积思维,暂不使用
if (board[a][b] == '1'){ //若格子为1
if ((a-startn+b-startm) % 2 == 0) tempvalue += 42; //且位于行+列为偶数的位置,正确,加上黑色格子的权值42
else tempvalue -= 42*i; //位置错误,减去i倍的黑色格子权值
}else{ //若格子为0
if ((a-startn+b-startm) % 2 == 0) tempvalue -= 42*i; //位置错误,减去i倍的黑色格子权值
else tempvalue++; //且位于行+列为奇数的位置,正确,加上白色格子的权值1
}
}
}
if (tempvalue == kernelvalue){ //若该核的实际值与期望值相等,则可表明每一位都与正确的核相等,即为要找的棋盘
maxn = i; //赋值最大尺寸
flag = 0; //标记大循环结束
count++; //顺便利用当前循环统计最大尺寸的数量
}
if (startm + i + 1 > n){ //如果列数无法移动
if (startn + i + 1 > n) break; //且行数也无法移动,则当前阶数的核已遍历完成,退出小循环,进行下一个阶数的核的遍历
else{ //如果行数还能移动
d++; //下移
startn = d;
startm = 0;
}
}else startm++; //如果列数还能移动,右移
}
}
cout << maxn << " " << count << endl;
return 0;
}暴力搜索法(全对)
#include <iostream>
using namespace std;
int main(){
ios::sync_with_stdio(false);
int n;
cin >> n;
char board[n][n];
for (int i = 0; i < n; i++) cin >> board[i];
int maxn = 0, count = 0, flag = 1, startn = 0, startm = 0, d = 0;
for (int i = n; i > 0; i--){
startn = 0;startm = 0;d = 0;
if (flag == 0) break;
while (1){
int is=1;
for (int a = startn; a < startn + i; a++){
for (int b = startm; b < startm + i; b++){
if(is==0) break;
if (board[a][b] == '1'){
if ((a-startn+b-startm) % 2 != 0){is=0;break;}
}else{
if ((a-startn+b-startm) % 2 == 0){is=0;break;}
}
}
}
if (is==1){
maxn = i;
flag = 0;
count++;
}
if (startm + i + 1 > n){
if (startn + i + 1 > n) break;
else{
d++;
startn = d;
startm = 0;
}
}else startm++;
}
}
cout << maxn << " " << count << endl;
return 0;
}8.Engine-字符串
思路:关键词和标题转成字母小写存入缓存变量再进行判断。
while True:
n = int(input())
if n == 0: # 遇0退出
break
paper = [] # 论文数据:[[标题,引用次数],...]
for i in range(n): # 读论文数据
title = input()
count = int(input())
paper.append([title, count]) # 存论文数据
m = int(input())
for i in range(m): # 读查询指令
keywords = input().lower().split(" ") # 按空格符分割关键词
result = [] # 查询结果
for j in range(n): # 对于数据库中的每篇论文
temp = paper[j][0].lower().split(" ") # 按空格符分割关键词
if len(keywords) == 1: # 如果查询的关键词只有一个
if keywords[0] in temp: # 判断该关键词是否在属于标题中的关键词
result.append(paper[j]) # 若属于则将该篇论文加入查询结果中
else: # 若关键词数量大于1个
flag = 1
for a in keywords: # 对于每个关键词
if a not in temp: # 如果其中任何一个不在标题关键词列表中
flag = 0 # 视为查询失败,退出循环
break
if flag == 1: # 若循环结束flag仍为1,则表明每个要查询的关键词都在标题中,加入结果列表
result.append(paper[j])
if len(result) != 0: # 若结果数量不为0,即能够查询到论文
result.sort(key=lambda x: x[1], reverse=True) # 将结果按照论文引用次数从大到小排列
for k in result:
print(k[0])
print("***")
else: # 若结果数量为0
print("") # 输出空行
print("***")
print("---") # 一组数据处理结束9.字符串压缩

思路:使用贪心法选择花费最少的方案进行压缩,同时为了避免贪心法得不到整体最优解,当遇到使用方案一编码时,逐个压缩,这样可以绕过方案二短见陷阱。
a, b = input().split(" ")[1:] # 获取a,b的值
a = int(a) # 转为整数类型
b = int(b)
s = input() # 读入字符串
substr = "" # 已压缩的字符串
coin = 0 # 最小硬币数量
startindex = 0 # 开始位置
endindex = 1 # 结束位置
temp1 = b # 方案二花费
temp2 = 0 # 方案一花费
while True: # 持续处理
if endindex == len(s)+1: # 若字符串已处理完毕则退出
break
if s[startindex:endindex] in substr: # 若子串在已压缩字符串中
if endindex != len(s): # 若未到末尾则继续查找,直到子串不在已压缩字符串中
endindex += 1
else: # 若已到结尾,则将其编码
temp2 = len(s[startindex:endindex])*a
if temp1 < temp2:
coin += temp1
else:
coin += temp2
endindex += 1
# 若子串不在已压缩字符串中,开始贪心法计算花费
elif endindex-startindex > 1:
temp2 = len(s[startindex:endindex-1])*a
if temp1 < temp2: # 若方案二花费小于方案一,则直接采用
coin += temp1
substr += s[startindex:endindex-1]
startindex = endindex-1
else: # 若方案一花费小于方案二,则先编码一个字符,再继续进行子串查找,可避免贪心法的弊端(即贪心法不一定得到整体最优)
coin += a
substr += s[startindex:startindex+1]
startindex += 1
elif endindex-startindex == 1:
coin += a
substr += s[startindex:endindex]
startindex += 1
endindex += 1
print(coin)10.拼写检查
思路:按题意依次操作即可。
dic = []
while True: # 读取第一部分数据
temp = input()
if temp == "#":
break
dic.append(temp)
while True: # 读取第二部分数据
temp = input()
find = []
if temp == "#":
break
if temp in dic: # 若词在字典中,则直接输出
print("{} is correct".format(temp))
continue
else: # 若不在字典中,进行三层判断
temp = list(temp) # 将字符串按字符展开为列表
for i in range(len(temp)): # 从单词中删除某个字母的情况
s = ""
for j in range(len(temp)):
if i == j:
continue
else:
s += temp[j]
if s in dic:
find.append(s)
for i in "abcdefghijklmnopqrstuvwxyz": # 用一个任意字母替换单词中的一个字母的情况
for j in range(len(temp)):
s = ""
for k in range(len(temp)):
if j == k:
s += i
else:
s += temp[k]
if s in dic:
find.append(s)
for i in "abcdefghijklmnopqrstuvwxyz": # 在单词中插入一个任意字母的情况
temp2 = temp.copy()
for j in range(len(temp)+1):
temp2 = temp.copy()
temp2.insert(j, i)
temp2 = "".join(temp2)
if temp2 in dic:
find.append(temp2)
if len(find) != 0: # 如果在字典中找到至少一个单词
find = list(set(find)) # 去重
index = []
for i in find:
index.append(dic.index(i))
sortfind = []
for i in range(len(find)):
sortfind.append([find[i], index[i]])
sortfind.sort(key=lambda x: x[1]) # 按在字典记录的顺序排序
words = []
for i in range(len(sortfind)):
words.append(sortfind[i][0])
temp = "".join(temp)
print("{}: {}".format(temp, " ".join(words)))
else: # 否则输出空
temp = "".join(temp)
print("{}:".format(temp))11.最小的K个数
思路: 将数存入列表中,使用集合操作去除重复值(将列表转为集合类型再转为列表类型,利用集合元素的唯一性,可去除重复值),找当前列表的最小数并输出,原列表中移出该最小数,继续上面的操作直到取出了足够数量的最小数。若原列表中的数的数量小于需要的数量,则只需输出(m=列表中数的数量)个数即可。
need = int(input().split(" ")[1]) # 获取第一行输入并按空格符分割字符串,取出第二个数据(即要求的最小数的数量),因为在Python中第一个数据无用
numbers = input().split(" ") # 获取第二行输入并按空格符分割字符串
numbers = list(set(numbers)) # 将列表转为集合类型再转为列表类型,利用集合元素的唯一性,可去除重复值
for i in range(len(numbers)): # 将每个数据转为整数类型
numbers[i] = int(numbers[i])
if need > len(numbers): # 若要求的数大于了现在列表中数的数量,则令其等于列表中数的数量
need = len(numbers)
for i in range(need): # 逐个输出最小值
num = min(numbers) # 找当前最小值
if i != need-1:
print(num, end=" ")
else:
print(num, end="")
numbers.pop(numbers.index(num)) # 移出该最小值12.绩点计算

思路: 题目不难,理解题意就好。(Python写的一直错三个样例,所以这题只能改用C++)
#include <iostream>
#include <iomanip>
using namespace std;
struct course{
int credit; //学分
int score; //成绩
double point; //绩点
};
int main(){
int n;
cin >> n;
course courses[n];
for (int i = 0; i < n; i++){
cin >> courses[i].credit;
}
for (int i = 0; i < n; i++){
cin >> courses[i].score;
if (courses[i].score >= 90 && courses[i].score <= 100)
courses[i].point = 4.0;
else if (courses[i].score >= 85 && courses[i].score < 90)
courses[i].point = 3.7;
else if (courses[i].score >= 82&&courses[i].score < 85)
courses[i].point = 3.3;
else if ( courses[i].score >= 78&&courses[i].score < 82)
courses[i].point = 3.0;
else if ( courses[i].score >= 75&&courses[i].score < 78)
courses[i].point = 2.7;
else if ( courses[i].score >= 72&&courses[i].score < 75)
courses[i].point = 2.3;
else if ( courses[i].score >= 68&&courses[i].score < 72)
courses[i].point = 2.0;
else if ( courses[i].score >= 64&&courses[i].score < 68)
courses[i].point = 1.5;
else if ( courses[i].score >= 60&&courses[i].score < 64)
courses[i].point = 1.0;
else
courses[i].point = 0.0;
}
double allpoint = 0, allcredit = 0, point = 0;
for (int i = 0; i < n; i++){
allcredit += courses[i].credit; //学分总和
allpoint += (courses[i].credit * courses[i].point); //绩点总和
}
point = allpoint / allcredit; //总评绩点
cout<<fixed<<setprecision(2)<<point<<endl;
return 0;
}13.xxx定律
思路: 算术题,递归求解。
def calculate(x):
global count # 引入全局变量
if x == 1: # 若x一开始就是1,则直接输出0
return 0
if x % 2 == 0: # 若是偶数
x /= 2
count += 1
else: # 若是奇数
x = (3*x+1)/2
count += 1
if x != 1: # 若处理后不等于1,递归
return calculate(x)
else: # 若等于1,输出步数
return count
count = 0 # 统计步数
while True:
n = int(input())
if n == 0: # 遇0退出
break
print(calculate(n)) # 计算步数
count = 0 # 重置步数14.数的距离差

思路: 算术题梅开二度,硬算即可。
numbers = input()
numbers = input() # 第一行输入没什么作用,直接input()两次读取数字即可
numbers = numbers.split(" ") # 以空格符分割文本
for i in range(len(numbers)): # 将文本形式的数字转为整数
numbers[i] = int(numbers[i])
numbers.sort() # 对数进行排序,后面通过下标可直接输出较小的值
Max = max(numbers) # 找最大值
Min = min(numbers) # 找最小值
d = [] # 存各个数的距离差
for x in numbers: # 求每个数的距离差
a = abs(abs(x-Max)-abs(x-Min)) # 题给公式
d.append(a) # 加入列表中
m = min(d) # 求最小距离差
mi = d.index(m) # 找到该最小距离差在d列表中的下标,此下标也对应着numbers列表中所求数的下标
print(numbers[mi])15.亲和数
思路: 对于输入的A、B两个数,分别求它们的所有约数并求和,判断是否等于另一个数,若双向相等,则为亲和数。求约数用模运算即可。
try:
while True: # 持续循环
Input = input().split(" ")
Sum = 0
for i in range(1, int(Input[0])): # 求所有约数之和
if int(Input[0]) % i == 0:
Sum += i
if Sum == int(Input[1]): # 若等于另一个数
Sum = 0
for i in range(1, int(Input[1])): # 再求另一个数的所有约数之和
if int(Input[1]) % i == 0:
Sum += i
if Sum == int(Input[0]): # 若等于另一个数
print("YES")
else:
print("NO")
except EOFError: # 若已经到输入的结尾EOF则退出
pass16.金币
思路: 每一次循环,金币总数增加i²,天数增加i,若增加后天数已经大于所给定的天数,则按照sum=sum-(增加后天数-给定天数)*i的规则求出实际金币总数。
try:
while True: # 持续循环
n = int(input())
Sum = 0 # 金币总数
Day = 0 # 天数
for i in range(1, n):
Sum += i*i
Day += i
if Day >= n: # 若增加后天数大于给定的天数
Sum -= (Day-n)*i # 金币退回
break
print("{} {}".format(n, Sum))
except EOFError: # 若已经到输入的结尾EOF则退出
pass17.小A的计算器

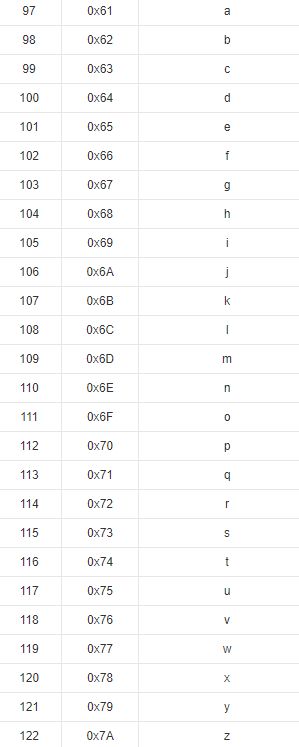
思路: 先将输入的两个26进制数转为10进制数然后相加,之后再转为26进制即可。可利用ASCII码表进行快速转换。用ord(X)-97可快速找出对应的十进制数。
n = int(input())
for i in range(n):
temp = input().split(" ")
s1 = 0 # 第一个数的十进制
rev1 = temp[0][::-1] # 逆序,方便从个位开始计算
for i in range(len(rev1)): # 将26进制数转为10进制数
s1 += (ord(rev1[i])-97)*pow(26, i)
s2 = 0 # 第二个数的十进制
rev2 = temp[1][::-1]
for i in range(len(rev2)):
s1 += (ord(rev2[i])-97)*pow(26, i)
s = s1+s2 # 求和
num = []
while s > 25: # 将10进制数转为26进制数
r = s % 26
num.append(chr(r+97))
s /= 26
num.append(chr(int(s)+97)) # 循环跳出后,还需处理一次
num.reverse() # 逆序,得到正确顺序的26进制数
print("".join(num)) # 将字母连接起来并输出18.小丑排序
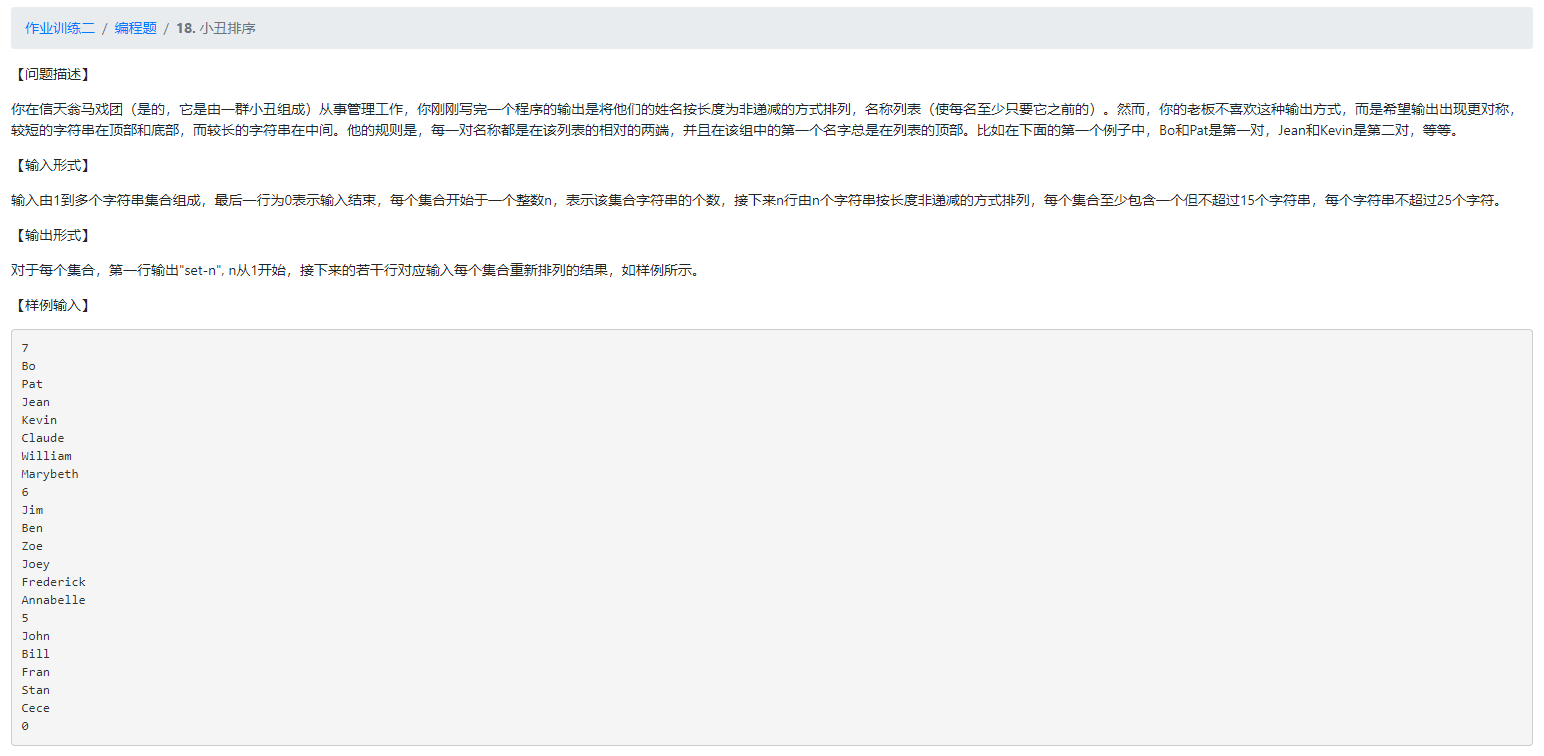
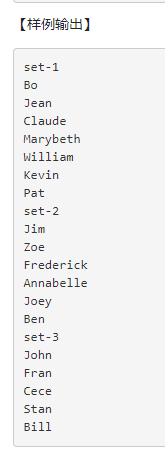
思路: 只需要将名字存入列表中,每次取出第一和第二个名字分别存入将要在头部输出和将要在尾部输出的列表中,然后原列表移出这两个数,重复上面的操作直到原列表的元素个数不大于1,最后顺序输出头部列表的元素,然后若原列表还存在1个元素也输出,再逆序输出尾部列表的元素即可(先入后出,所以要逆序)。
count = 1 # 输出数据组数
while True:
n = int(input())
if n == 0: # 遇0退出
break
names = [] # 名字列表
for i in range(n): # 存储名字
temp = input()
names.append(temp)
head = [] # 头部列表
tail = [] # 尾部列表
while len(names) > 1: # 若原列表中元素个数还大于1则执行
head.append(names[0]) # 原列表第一个元素加入头部列表
tail.append(names[1]) # 原列表第二个元素加入尾部列表
names.pop(0) # 移出第一个元素
names.pop(0) # 移出第二个元素
tail.reverse() # 尾部列表逆序
print("set-{}".format(count))
for i in head:
print(i)
if len(names) == 1:
print(names[0])
for i in tail:
print(i)
count += 119.数圈
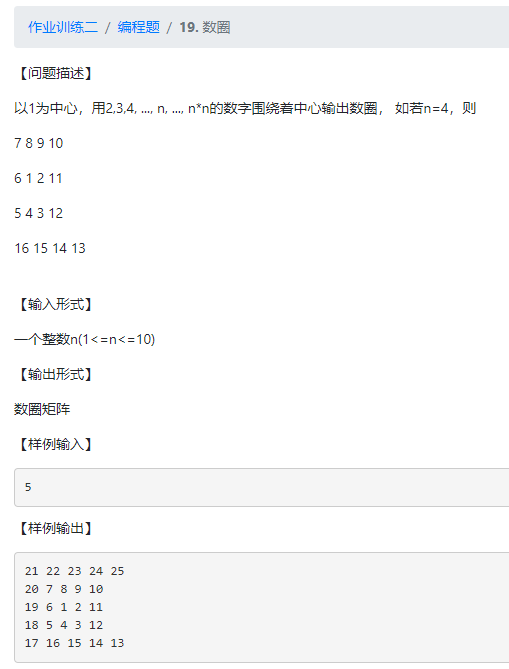
思路: 根据阶数的奇偶算出中心点1的位置,若阶数为偶数则中心点横纵坐标为int(t/2)-1,若为奇数则为int(n/2),用循环对矩阵绕着中心点1顺时针赋值,具体操作请看代码注释。
t = int(input())
if t % 2 == 0: # 若为偶数
center = int(t/2)-1 # 1的坐标
else: # 若为奇数
center = int(t/2) # 1的坐标
matrix = [[0 for a in range(t)] for b in range(t)] # 生成一个t*t矩阵
num = 1 # 下一个要赋值的数
n = center # 下一个赋值点的行
m = center # 下一个赋值点的列
matrix[n][m] = num # 初始化赋值
m += 1 # 初始化移位
num += 1 # 初始化增值
direction = "down" # 下一个移动方向
count = 2 # 按照方向移动的格数
tempcount = 2 # 用于判断是否移动了足够的次数,为0时则以移动次数够了
change = 0 # 用于记录方向改变的次数
nextdirection = {"right": "down", "down": "left",
"left": "up", "up": "right"} # 当前方向的下一个方向,顺时针
while num <= t*t: # 当数还未大于t的平方时,循环继续,对矩阵绕着中心1按顺时针赋值
matrix[n][m] = num
tempcount -= 1
num += 1
if tempcount == 0: # 更换方向
direction = nextdirection[direction]
change += 1
tempcount = count
if change == 2: # 移动格数增加
count += 1
change = 0
if direction == "right":
m += 1
elif direction == "down":
n += 1
elif direction == "left":
m -= 1
elif direction == "up":
n -= 1
for i in range(t): # 将矩阵中的数转为字符串类型
for j in range(t):
matrix[i][j] = str(matrix[i][j])
for i in matrix: # 按行输出
print(" ".join(i))20.锤子剪刀布
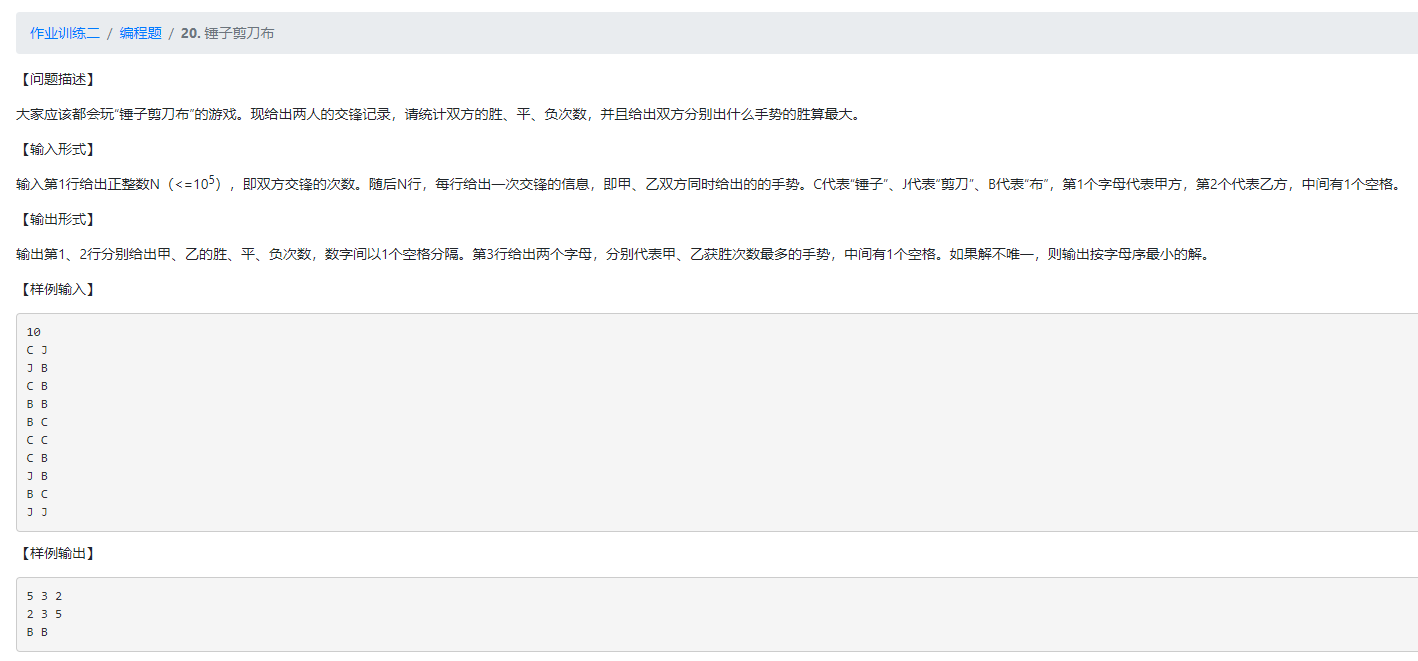
思路: 需要记录甲的胜、平、负的场数,逆序即可得到乙的场数。还要记录甲和乙获胜的手法的次数,求最大值即可,为了能按照字典序小的输出,将列表定为[0,0,0]对应["B","C","J"]。
n = int(input())
win = 0 # 甲的胜场
loss = 0 # 甲的负场
equal = 0 # 甲的平场
data = [[0, 0, 0], [0, 0, 0]] # 按照“BCJ”的下标顺序记录甲和乙的手法的胜场次数
for i in range(n): # 胜负判断
temp = input().split(" ")
if temp[0] == temp[1]:
equal += 1
if temp[0] == "C" and temp[1] == "J":
win += 1
data[0][1] += 1
elif temp[0] == "C" and temp[1] == "B":
loss += 1
data[1][0] += 1
elif temp[0] == "J" and temp[1] == "C":
loss += 1
data[1][1] += 1
elif temp[0] == "J" and temp[1] == "B":
win += 1
data[0][2] += 1
elif temp[0] == "B" and temp[1] == "C":
win += 1
data[0][0] += 1
elif temp[0] == "B" and temp[1] == "J":
loss += 1
data[1][2] += 1
wel = [str(win), str(equal), str(loss)]
print(" ".join(wel)) # 甲的胜平负
wel.reverse() # 逆序
print(" ".join(wel)) # 乙的胜平负
i = data[0].index(max(data[0])) # 找到甲的胜场最多的手法
j = data[1].index(max(data[1])) # 找到乙的胜场最多的手法
if i == 0:
print("B", end=" ")
elif i == 1:
print("C", end=" ")
else:
print("J", end=" ")
if j == 0:
print("B", end="")
elif j == 1:
print("C", end="")
else:
print("J", end="")21.新型冠状病毒(COVID19)传播
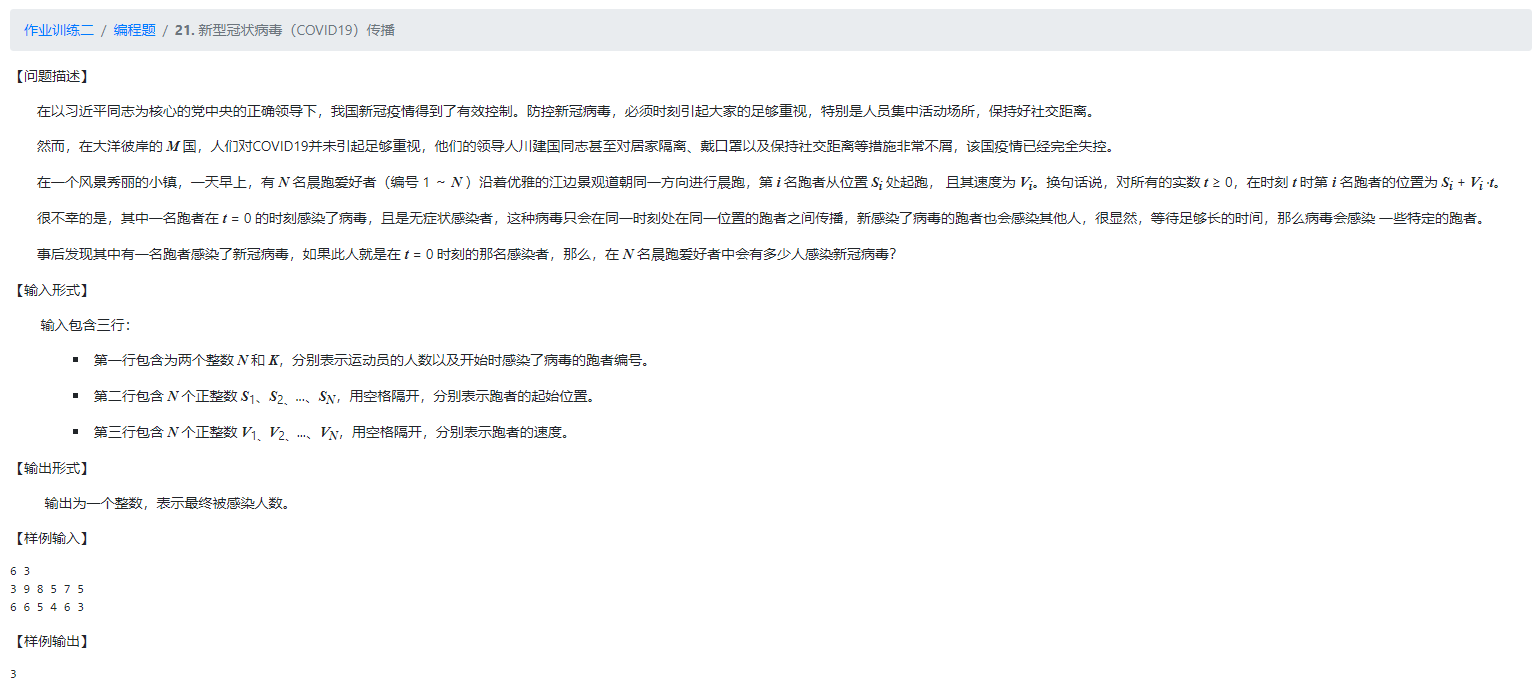
思路:这是一个时间不限的追及问题,若位置位于最初感染者的左边且速度比他大,则必定会感染,若位置位于最初感染者的右边且速度比他小,也必定会感染。那么可以想到,某个人如果想要始终都不被感染,只有两种情况:1.位于最初感染者的左边,且其速度小于以最初感染者为中心分隔的选手队列的右边的最小的速度,这样他就不会因为追上被感染者而感染。2.位于最初感染者的右边,且其速度大于左边的最大的速度,这样他就不会因为被前面的交叉感染者追上而被感染。故对读入数据按位置从小到大,速度从大到小(因为可能存在位置与最初感染者相同且速度大于他的情况,可避免后续查找左边最大速度时出错)排列,查找左边最大速度和右边最小速度,再进行上述的判断找到始终不会被感染的人并统计数量,最后用总人数减去安全人数即可得到被感染人数。处理时要注意超大规模数据的读入问题,使用ios::sync_with_stdio(false);关闭输入同步,可大大提高运行效率,cin是一个很慢的输入操作。结构体数据在最开始就定义尺寸为10的7次方,因为不这么做后三组测试数据会出现数组越界,具体原因不明。
#include<iostream>
#include<algorithm>
using namespace std;
struct player{ //选手信息
int index; //编号
int position;//起始位置
int speed; //速度
};
bool compare(const player &data1,const player &data2)
{
if(data1.position==data2.position)
{
return data1.speed>data2.speed; //速度从大到小排序,因为可能存在位置与最初感染者相同且速度大于他的情况,可避免后续查找左边最大速度时出错
}
return data1.position<data2.position; //位置从小到大排列
}
const int size=10000000;
player data[size]; //题目最大数据量为10^7,所以预创建这么大的结构体数组
int main(){
ios::sync_with_stdio(false); //关闭输入同步,加快数据读入时间
int n,p;
cin>>n>>p;
for(int i=0;i<n;i++){
cin>>data[i].position;
data[i].index=i+1;
}
for(int i=0;i<n;i++){
cin>>data[i].speed;
}
sort(data,data+n,compare); //对数据排序
int count=0; //始终不会被感染的人的数量
int rightmin=10000; //以最初感染者为中心的右边选手中的最小速度值
int leftmax=-1; //以最初感染者为中心的左边选手中的最小速度值
int x; //遍历缓存量,第一个循环结束后x即为最初感染者的下标
for(x=0;x<n;x++){
if(data[x].speed>leftmax){ //寻找左边最大速度
leftmax=data[x].speed;
}
if(data[x].index==p){ //若位置已是最初感染者则退出
break;
}
}
for(int i=x;i<n;i++){
if(data[i].speed<rightmin){ //寻找右边最小速度
rightmin=data[i].speed;
}
if(data[i].position>data[x].position&&data[i].speed>=leftmax){ //同时找出右边始终不会被感染的人并统计数量
count++;
}
}
for(int i=0;i<x;i++){
if(data[i].position<data[x].position&&data[i].speed<=rightmin){ //找出左边始终不会被感染的人并统计数量
count++;
}
}
cout<<n-count<<endl; //输出总人数减去安全的人数即可得到感染的人数
return 0;
}
一袍清酒付 · 2021-07-15 08:26
飞行棋那个题目,在题中要求如果一个格子里面有两个棋子的话,就要将先在里面的棋子返回第0格,少了个判断,虽说再OJ上确实没什么问题,但是严谨点较好啦!
B1ue1nWh1te · 2021-07-15 18:25 作者
是的,谢谢指正,之前写题的时候发现全对就没管了- - 这个情况确实需要考虑才符合题意
进一寸有进一寸的欢喜 · 2021-07-10 23:19
正好也在学python,关注着森海的更新~我要加油
B1ue1nWh1te · 2021-07-11 16:11 作者
谢谢这位朋友,继续加油。(计算机圈子里我叫B1ue1nWh1te,群里的森海是我的小号hhh)